Description of the «TokenRing» model
This model is presented here. We consider a system where a set of machines are places in a ring, numbered 0 to N. Each machine i only knows its own state and the state of its left neighbor, i.e., machine (i-1)%(N+1). Machine number 0 plays a special role, and it is called "the bottom machine". The state of each machine is an integer number in [0, N]. We will note S(i) the state of machine i.
Each machine may determine if it has a so-called "privilege" based on its state and the one of its left neighbor. A privilege is in this context the right to perform an operation. After performing its operation, the machine updates its own state, and may loose its privilege.
The objective of the protocol is to reach a stable state for the system. In a stable state:
-
there is a unique machine with a privilege, -
any subsequent state is also a stable state.
Furthermore, the protocol ensures non-starvation: at any time, any machine is sure to have a privilege after a finite number of steps.
The detail of the protocol is different for the bottom machine, and the other machines:
-
The bottom machine has the privilege if its left neighbor state is equal to its own state. In this case, the bottom machine updates its status by incrementing it: if S(N) = S(0) then S(0) := (S(0) + 1) % N
-
Any other machine i > 0 has the privilege if its left neighbor state is different from its own state. In this case, machine i updates its status by setting it to the value of the left machine: if S(i-1) != S(i) then S(i) := S(i-1).
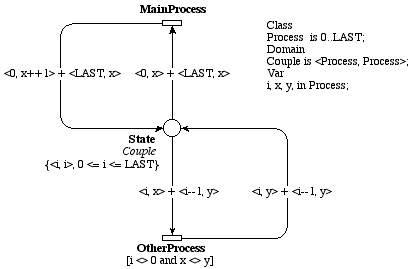
The figure above shows this model and is set up for LAST+1 machines.
Scale factor
The scale factor is the number of machines. Proposed instances of this models contain the following numbers: 5, 10, 15, 20, 30, 40, 50, 100, 200, 300, 400, 500.
Model files
PNML files and a set of properties respecting the BNF we propose are available in the submission kit.
